请问最近几年比较新的多目标优化算法都有什么?
想试一下自己的优化算法跟其他算法的指标对比,目前是想跟mopso,nsga2、moea\\d进行比较,不过这几个都比较老,请问有没有较新一点的有代表性的多目标优化算法算法呢
浣熊优化算法(Coati Optimization Algorithm,COA)由Dehghani Mohammad等人于2022年提出的模拟浣熊狩猎行为的优化算法,该算法具有进化能力强,收敛速度快,收敛精度高等特点。
COA具体原理如下: 智能优化算法:浣熊优化算法-附代码_智能算法研学社(Jack旭)的博客-CSDN博客
参考文献:Dehghani Mohammad, Montazeri Zeinab, Trojovská Eva, Trojovsky Pavel. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems[J]. Knowledge-Based Systems,2023,259.


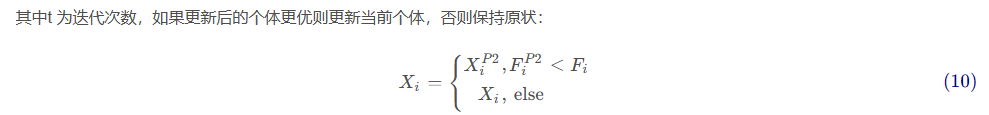
多目标浣熊优化算法(Multi-objective Coati Optimization Algorithm,MOCOA)由COA融合多目标策略而成,为了验证所提的MOCOA的有效性,将其在46个多目标测试函数(ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3)以及1个工程应用(盘式制动器设计)上实验,并采IGD,GD,HV,SP四种评价指标进行评价。
部分代码:
close all;
clear ;
clc;
reference code link: https://mbd.pub/o/bread/ZJqVlJlu
% TestProblem测试问题说明:
%一共46个多目标测试函数(1-46)+5个工程应用(47-50),详情如下:
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12:DTLZ1-DTLZ7
%13-22:wfg1-wfg10
%23-32:uf1-uf10
%33-42:cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
%47 盘式制动器设计 https://blog.csdn.net/weixin_46204734/article/details/124051747
reference code link: https://mbd.pub/o/bread/ZJqVlJlu
TestProblem=1;%1-47
MultiObj=GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np=200; % Population size 种群大小
params.Nr=200; % Repository size 外部存档中最大数目,可适当调整大小,越大,最终获得的解数目越多
params.maxgen=200; % Maximum number of generations 最大迭代次数
reference code link: https://mbd.pub/o/bread/ZJqVlJlu
REP=MOCOA(params,MultiObj);
%% 画结果图
figure
if(size(REP.pos_fit,2)==2)
h_rep=plot(REP.pos_fit(:,1),REP.pos_fit(:,2),'ok'); hold on;
if(isfield(MultiObj,'truePF'))
h_pf=plot(MultiObj.truePF(:,1),MultiObj.truePF(:,2),'.r'); hold on;
legend('MOCOA','TruePF');
else
legend('MOCOA');
end
grid on; xlabel('f1'); ylabel('f2');
end
if(size(REP.pos_fit,2)==3)
h_rep=plot3(REP.pos_fit(:,1),REP.pos_fit(:,2),REP.pos_fit(:,3),'ok'); hold on;
if(isfield(MultiObj,'truePF'))
h_pf=plot3(MultiObj.truePF(:,1),MultiObj.truePF(:,2),MultiObj.truePF(:,3),'.r'); hold on;
legend('MOCOA','TruePF');
else
legend('MOCOA');
end
grid on; xlabel('f1'); ylabel('f2'); zlabel('f3');
end
title(MultiObjFnc)
reference code link: https://mbd.pub/o/bread/ZJqVlJlu
Obtained_Pareto=REP.pos_fit;
if(isfield(MultiObj,'truePF'))%判断是否有参考的PF
True_Pareto=MultiObj.truePF;
%% Metric Value
% ResultData的值分别是IGD、GD、HV、Spacing (HV越大越好,其他指标越小越好)
ResultData=[IGD(Obtained_Pareto,True_Pareto),GD(Obtained_Pareto,True_Pareto),HV(Obtained_Pareto,True_Pareto),Spacing(Obtained_Pareto)];
else
%计算每个算法的Spacing,Spacing越小说明解集分布越均匀
ResultData=Spacing(Obtained_Pareto);%计算的Spacing
end
%%
% Display info
disp('Repository fitness values are stored in REP.pos_fit');
disp('Repository particles positions are store in REP.pos');
部分结果:
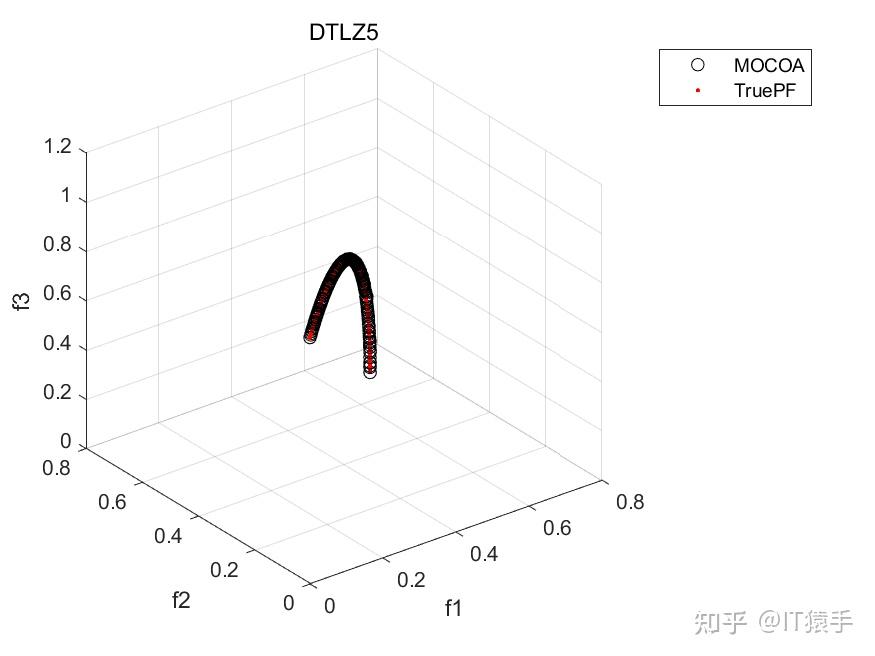
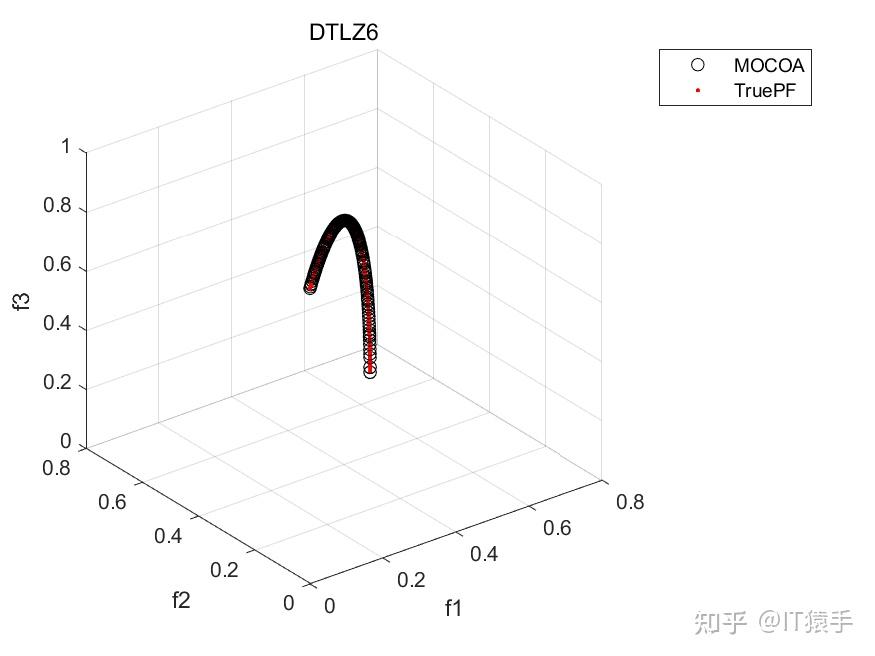
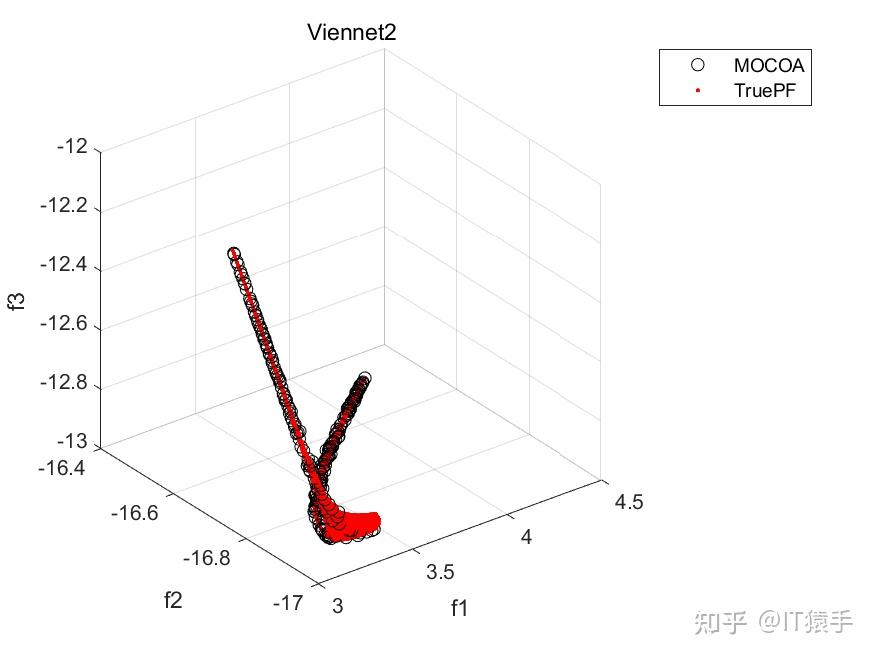
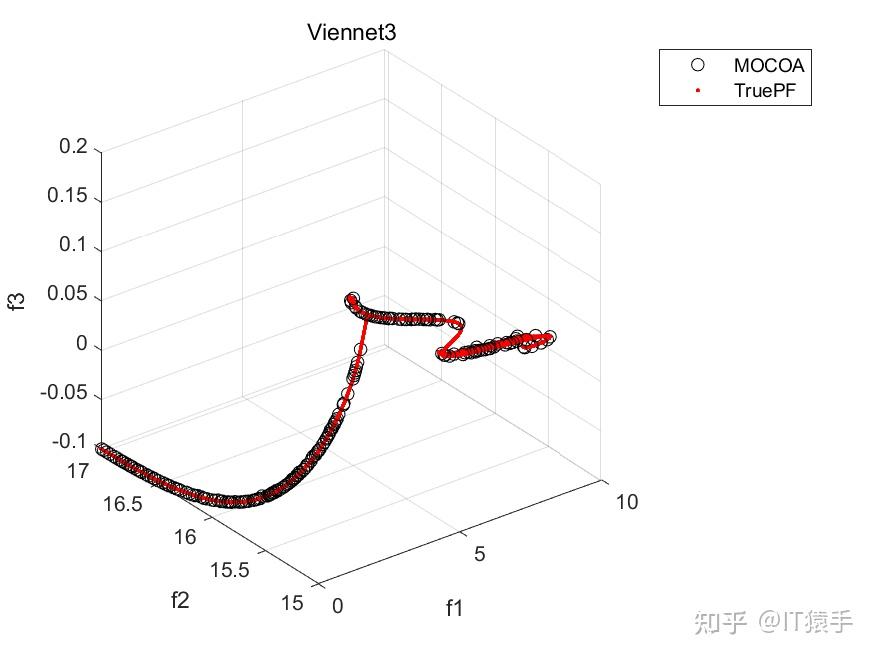

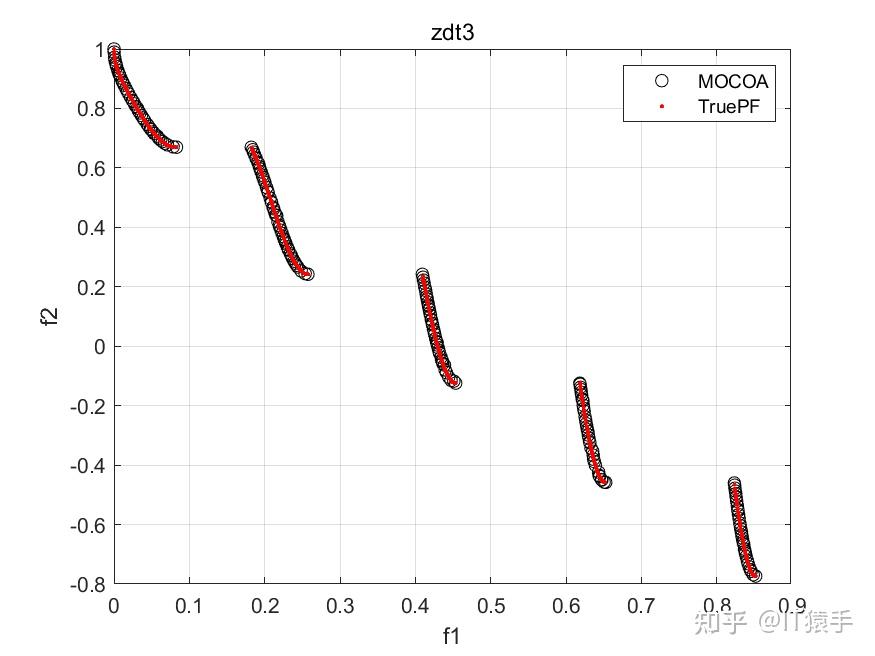
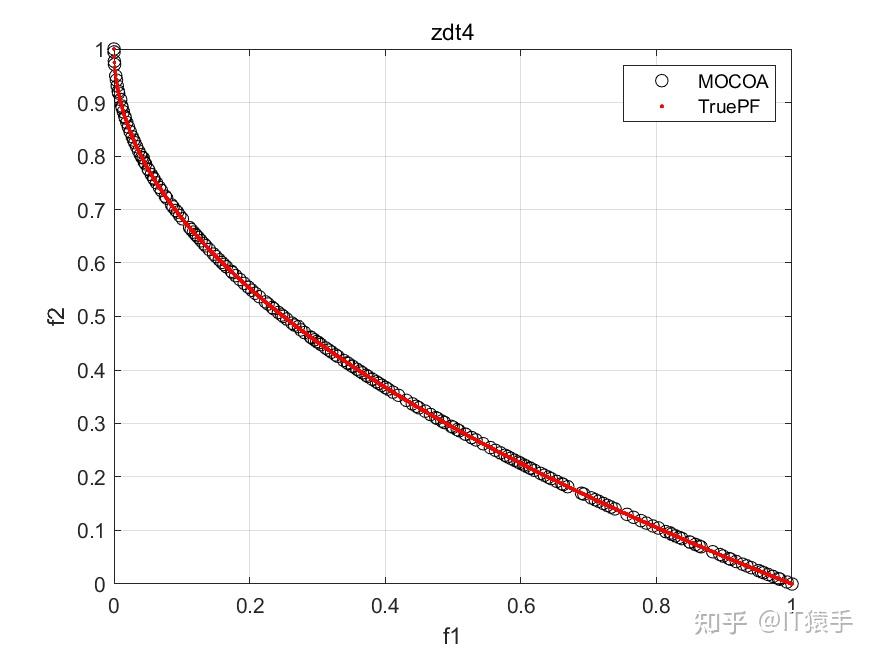

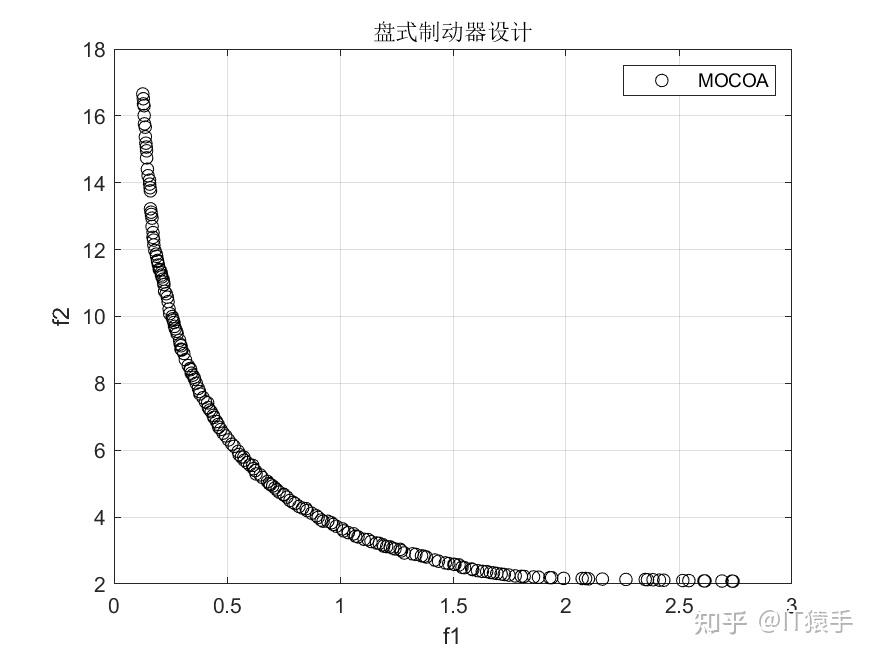
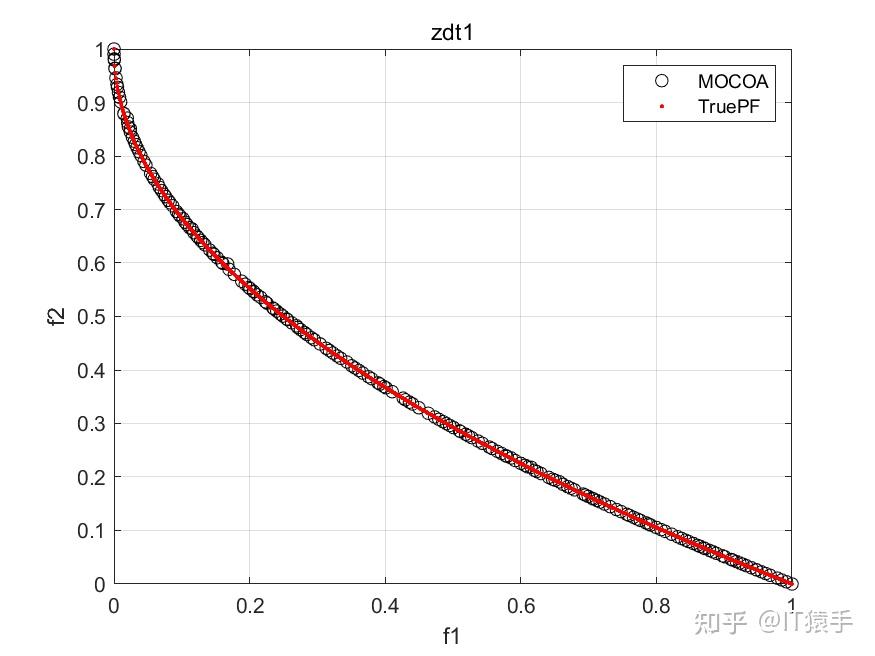
基于“俄罗斯轮盘赌”的并行演化方法参见https://www.zhihu.com/question/634730092/answer/3324614316?utm_psn=1718391023175049216
?前面的文章里作者介绍了多目标灰狼优化算法(Multi-Objective Grey Wolf Optimizer,MOGWO),该算法是由Mirjalili等(灰狼算法的提出者)于2016年提出[1],发表在中科院一区期刊《expert systems with applications》。
MOGWO保留了灰狼算法的种群更新机制,即通过模拟灰狼的严格等级制度以及自然界中的狩猎和捕食行为来迭代搜索优化,因此具有收敛速度快、效率高以及精度高等优点。当然,每种元启发式算法都不是完美的,面对复杂高维问题,MOGWO也会有早熟收敛、陷入局部最优等问题。因此本文从以下几个方面对MOGWO进行改进:收敛因子、种群初始化、围猎机制、头狼更新
00 文章目录
1 多目标灰狼优化算法原理
2 改进的多目标灰狼优化算法
3 代码目录
4 算法性能
5 源码获取
01 多目标灰狼优化算法原理
多目标灰狼优化算法的原理在作者往期文章已经作出介绍
02 改进的多目标灰狼优化算法
首先,对于原MOGWO算法,其在Archive中选择头狼的方式上提高了算法的搜索性能,然而若Archive种群陷入局部最优,则算法将难以跳出;其次,初始种群的随机生成,偶然性强,容易出现种群分布不均匀,降低种群多样性;同时,灰狼算法虽然有较快的收敛速度,但其收敛精度仍有一定提升的空间。基于以上认识,本文对MOGWO作出以下改进:
2.1 量子位Bloch球面初始化种群
高质量的初始种群对算法的收敛速度和求解质量有很大的帮助,而由于MOGWO采用随机生成初始种群的方法,容易出现种群分布不均匀,会导致种群多样性减少,种群质量不高,影响算法的收敛速度。因此本文采用量子位Bloch球面初始化种群,下面介绍其原理:
在量子计算中,信息的最小单位是量子比特。量子比特的状态可以表示如下
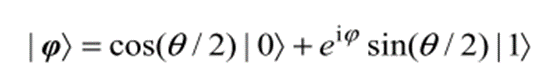
其中,等式右边的两个参数可以唯一确定Bloch球面上的一点P。
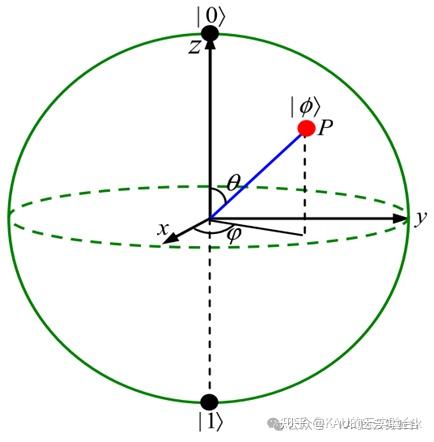
[图源:Quantum Particle Swarm Optimization Based on Bloch Coordinates of Qubits]
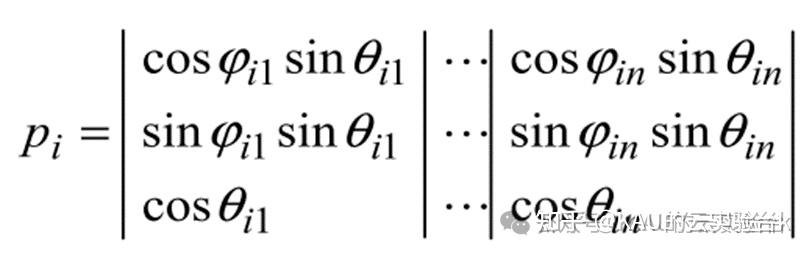
因此,任何量子位都可以与Bloch球面上的一点对应,又由于Bloch球面是一个三维单位球面,则量子位的球面坐标可以表示为:
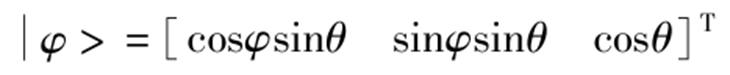
于是,灰狼个体可以采取量子位的Bloch球面坐标编码,设Pi为种群中第i个个体,n为优化维数,则其编码描述如下
其中,参数分别为在[0,2pi]和[0,pi]之间的随机数。可以将量子位的三个坐标看作三条并列的基因链,每个基因链都可代表一个解,则个体可以同时表示三个解,定义为x、y、z解:
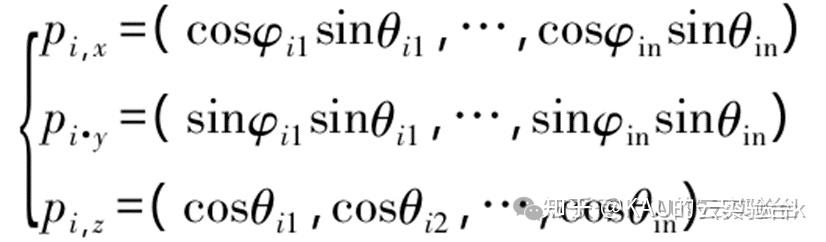
量子比特编码的个体可以表示为:
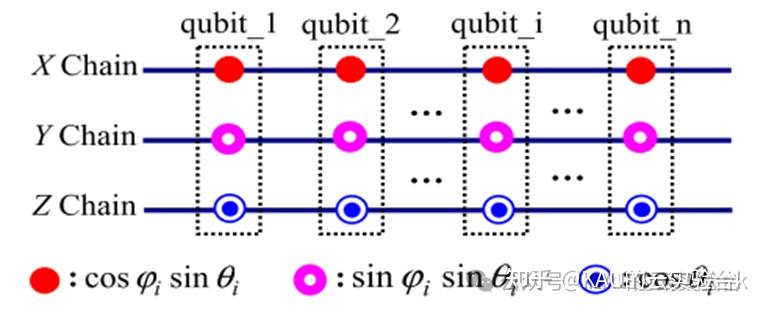
[图源:Quantum Particle Swarm Optimization Based on Bloch Coordinates of Qubits]
一个量子位含3个Bloch坐标,每个坐标又可以代表一个解,而Bloch坐标下每维的范围是[-1,1],因此需要进行变换以对应到所需要的解空间。记个体i第j个量子位的Bloch坐标为[Xij,Yij,Zij],则对应到解空间为:
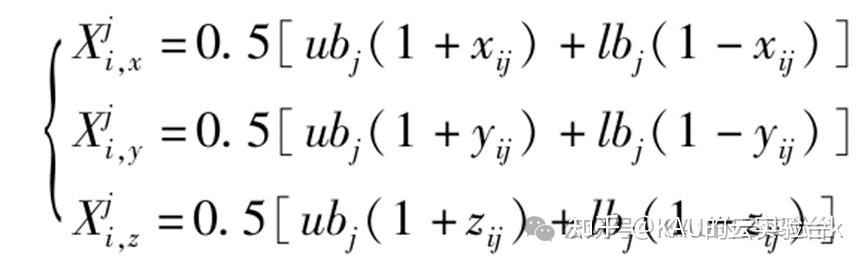
其中,[lbj,ubj]为对应变量的上下界。
由此可得到三个可行解,其适应度最佳者则可作为该个体的编码,由此能够提高和改善初始种群在搜索空间上的分布质量,加强其全局搜索能力。
2.2 非线性收敛因子
在GWO算法中,A是控制灰狼群体狩猎的重要参数。
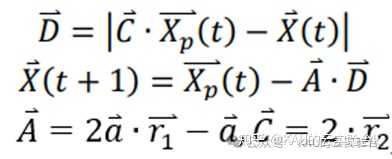
当|A| >1时,灰狼群体倾向于大范围的全局搜索;当|A| <1时,灰狼群体将攻击猎物,即在最优解附近进行局部搜索。
而收敛因子a的将变化直接影响参数A的取值变化,在原GWO中,a从2线性减小到0,但面对复杂问题时,线性递减的策略往往易使群体不能充分探索空间,我们希望在前期a保持较大的值,以对空间进行充分的全局探索,而在后期a能保持较小的值使算法倾向于局部开发,加快收敛速度。由此提出一种非线性的收敛因子,公式略..
改进前后的收敛因子变化情况如下:
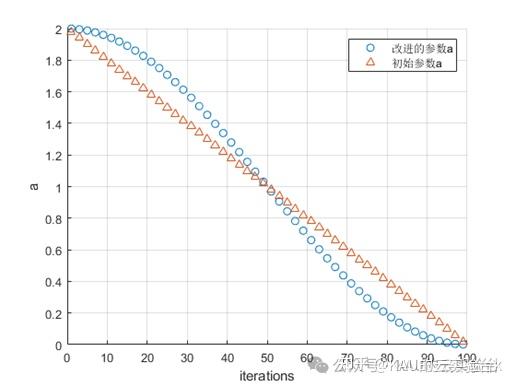
2.3 融合蝠鲼觅食的灰狼围猎
在原GWO 算法中,种群信息没有得到充分利用,这是由于个体位置更新仅由三个头狼引导,这意味着灰狼个体总是围绕头狼,此方法虽然有利于收敛,但若头狼陷入局部最优时,种群的进化将陷入停滞。
为了加强种群间的信息交流,受蝠鲼觅食优化算法启发,设计了一种新的位置更新公式,公式前半部分有助于算法快速收敛到最优解,后半部分有助于提高种群多样性以避免过早成熟。公式略..
在前期,个体的社会学习能力强,并且也保证了对全局最优位置的勘探能力,增强了对搜索空间的覆盖性,后期则倾向于在头狼附近搜索,加快收敛。
2.4 联想学习更新Archive
MOGWO中的外部档案Archive存储种群中的非支配解,在迭代前期,该机制能够有效保留精英级信息,但随着迭代的进行,非支配解数量将急剧增加,虽然其中的拥挤距离删除能够在一定程度上保证解集的质量,但仍会丢失部分优解信息,并且迭代后期大量相似解的充斥可能会诱使种群陷入局部最优,因此本文将对Archive中的解进行扰动变异,以增强解集多样性。
联想学习是近年提出的一种更新策略,可以提高算法的探索性能[2]。因此本文将联想学习引入对Archive中的部分个体进行更新,公式略..
2.5 算法流程
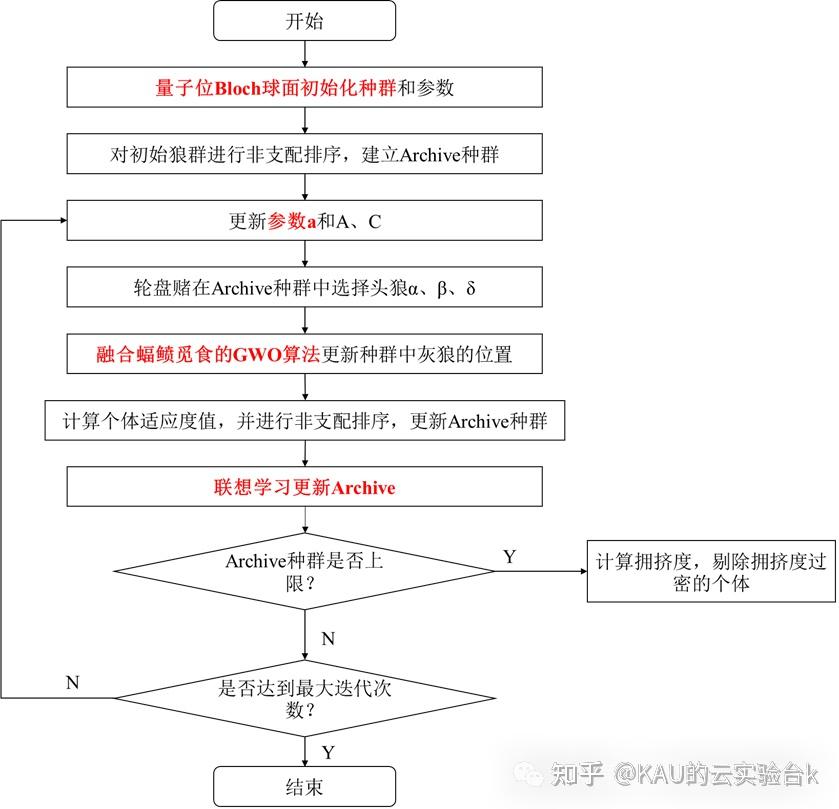
03 代码目录
代码包含两个部分,一部分为仅运行改进多目标灰狼优化算法的程序集,方便工程修改;另一部分为与其他算法有对比的程序集,完整代码目录如下:

Only_MAQMOGWO
perf_compare
代码注释完整,其中部分改进算法的程序如下:
04 算法性能
4.1 测试函数
采用3个无约束的多目标优化问题的测试函数ZDT1-3对算法进行性能测试:
主要来自参考文献:
Zitzler E, Deb K, Thiele L. Comparison of multi-objective evolutionary algorithms: Empirical study[J]. Evolutionary Computation, 2000, 8(2): 173-195.
(1)ZDT1
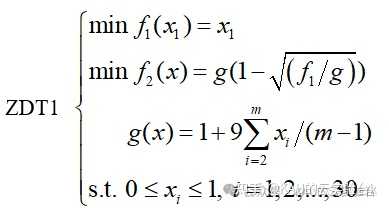
m=30,目前已知的Pareto前端的特征:凸的
(2)ZDT2
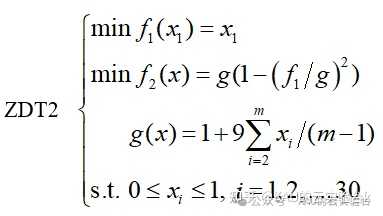
m=30,目前已知的Pareto前端的特征:凹的
(3)ZDT3
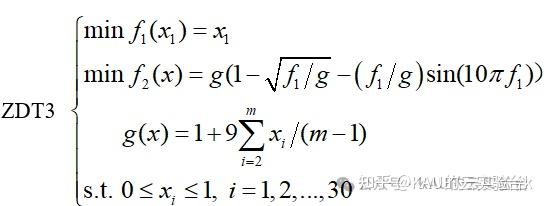
m=30,目前已知的Pareto前端的特征:非连续的
4.2 评价指标
采用IGD、GD、HV、SP这4个指标对解集的收敛性、均匀性和广泛性进行量化分析,各指标计算方式如下:
4.2.1 反世代距离(inverted generational distance, IGD)
IGD能够对算法的收敛性和分布性进行比较和评价,主要通过计算每个在真实 Pareto 前沿面上的参考点到算法获取的个体外部空间映射之间的最小距离和,来评价算法的收敛性能和分布性能。IGD值越小,则算法得到的最优解集越靠近真实Pareto前沿:
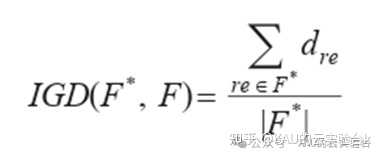
式中:F*为真实Pareto前沿;F为算法得到的最优解集;dre为Pareto最优面上点re与算法最优解集中个体i的最小欧式距离。
4.2.2世代距离(generational distance,GD)
用于评价所求得的近似Pareto前沿相对真实 Pareto前沿的逼近程度,也即收敛性,定义为:
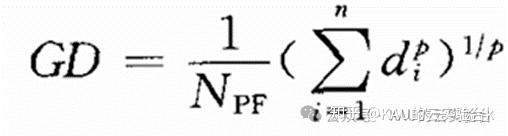
其中,NPF为近似Pareto前沿中个体的数量;p=2;d为真实 Pareto前沿中第 i个个体的目标向量到近似Pareto前沿最近个体的欧氏距离。GD越小,表明收敛性越好。
4.2.3空间度量(spacing,SP)
用于评价所求得的近似Pareto前沿的分布情况,其定义为:
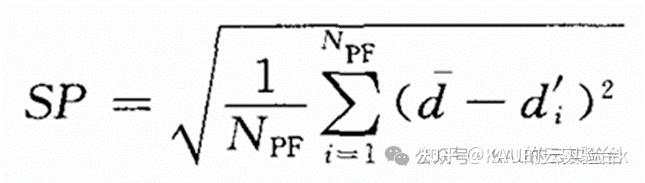
SP越小,表明近似Pareto前沿的分布越均匀,分布性越好。
4.2.4超体积(hypervolume,HV)
超体积又被称为 S 度量或勒贝格测度,表示的是近似集与参考点在目标空间中围成的区域的体积,用于评价目标空间被一个近似集覆盖的程度。给定一个参考点 r 和一个由算法获得的近似集 A,则 HV的计算公式如下所示:
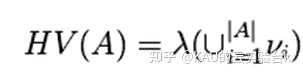
其中,λ代表勒贝格测度,νi代表参考点 r 和近似集 A 中的非支配个体构成的超体积。HV 值越大说明算法的综合性能越好。尽管 HV由于其严格符合帕累托一致原则且无需已知真实的Pareto 前沿面被广泛地使用,但其仍然具有一些不可避免的缺陷。
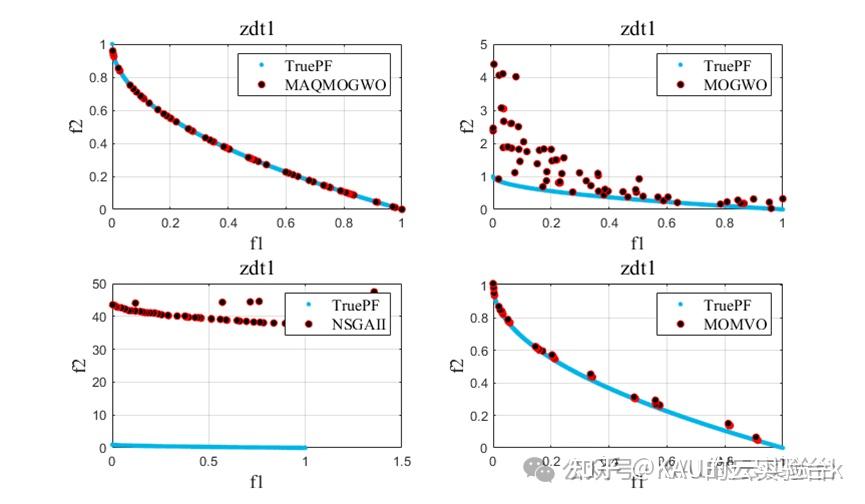
4.3 结果对比
引入MOGWO、MOMVO(多目标多元宇宙优化算法)和NSGAII进行对比实验,得到结果如下:
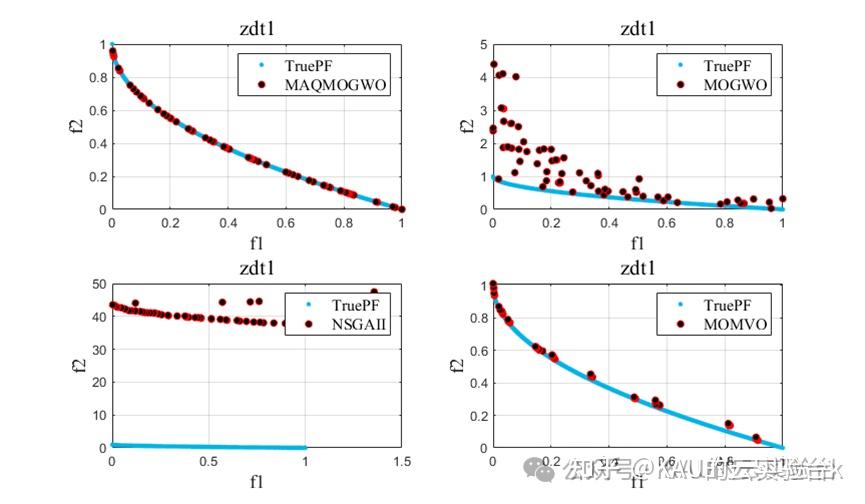
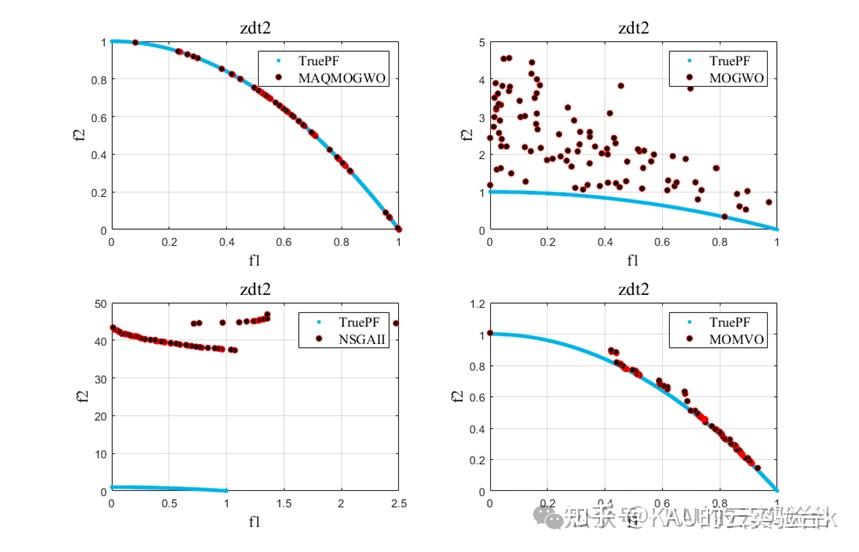
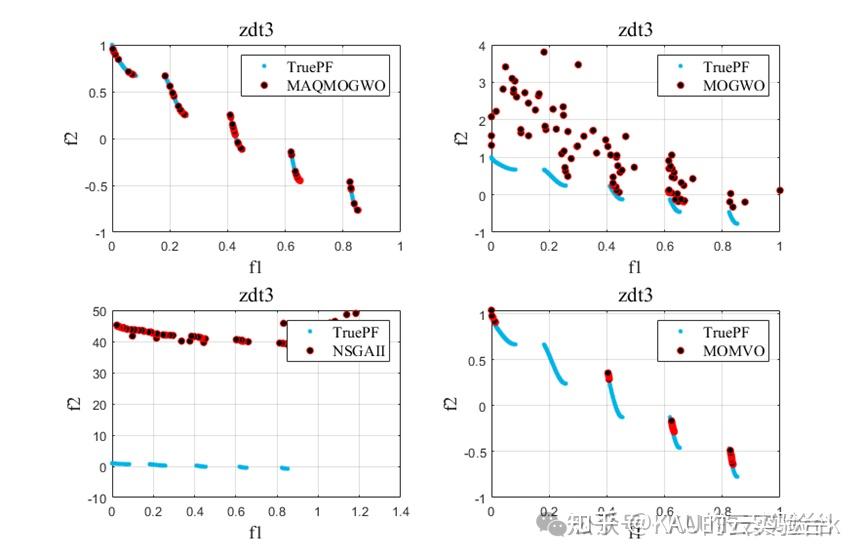

改进的算法性能得到了提升。
最后,在多目标算法中,虽然Pareto支配解和非支配解排序的方法十分常见且经典,但当客观维度增加时,越来越多的个体不受彼此支配,这将大大增加了非支配排序方法的选择压力,因此可以考虑新的控制方式用于处理高维目标问题。
05 源码获取
在GZH(见 简介)后台回复“MAQMOGWO”
参考文献
[1]Mirjalili S,Mirjalili S M .Lewis A. Multi-objective grey wolf optimizer : A novel algorithm for multi-criterion optimization[J]. Expert Systems with Applications.2016,47:106-119
[2]A. A. Heidari,I. Aljarah,H. Faris,H.Chen,J. Luo,and S. Mirjalili,“An enhanced associative learning-based exploratory whale optimizer for global optimization,”Neural Comput.Appl., vol. 32, no. 9, pp. 5185-5211,May 2020.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看 (?_)?(不点也行)



