拓扑学｜笔记整理（4）——引入，基，常见拓扑举例

（已经过第一次修改，修改了两个术语的中文翻译）

大家好！

评论和私信有人和我说点集拓扑太慢要我更代数拓扑……这里说一下哈：拓扑学是我们学校下学期数学专业的专业课。因此寒假的自学很大一部分是服务于下学期的。代数拓扑的内容我的专业倾向的用处不大，所以最近更新代数拓扑内容的可能性不大，还请大家谅解哈。

因为最近GRE班开课，这两天是暴雪天，刚去拿到驾照（路上摔了好几次呢），又有一大堆GRE的作业，导致笔记更新的速度慢了点。没事，后面还是有希望正常速度更新的，大家不用着急哈。

提供之前的笔记：

• 拓扑学|笔记整理（1）——集合，函数，关系
• 拓扑学|笔记整理（2）——数域系统，笛卡尔积，有限集
• 拓扑学|笔记整理（3）——无限集，可列集，选择公理，良序集

我们开始今天的内容。

• 拓扑空间（引入）
• 拓扑的基
• 常见拓扑举例（上）——实数轴拓扑，序拓扑

从这一节开始，应该算是正式的买入了拓扑的大门，研究拓扑学的方法和思路，其实我个人认为比较抽象，因此画风更像是抽象代数的画风。当然了，从拓扑本身的用处来看，它确实也可以导出很多有趣的东西，不过这是后话了。

为了方便

首先给出拓扑的定义。

Definition:topology,topological space
定义一个在集合 上的拓扑 为一系列 的子集合的集合，含有如下性质：
(1)
(2) 中的任意集合的元素的并集合仍然属于 。
(3) 中的任意集合的元素的有限交集合仍然属于 。
并且，这个拓扑对应的集合 称为拓扑空间。

这里需要说明几点。

因为在集合论中，对于collection一词如何翻译，一直存有争议。为了方便理解，不引入新的概念，我一直使用的是“集合的集合”的说法。因此这个定义要说清楚就出现了困难，也不方便于之后的介绍。所以我们在这里修改它的称呼为“族”，来称呼之前说的“集合的集合”。并且重新添加一些新的定义帮助理解：

1. 族(collection)用来表示元素仍然为集合的集合。
2. 子族(subcollection)：族的子集，仍然是族。

这样，其实最后的两条定义，部分地方在语言修饰上可以这么改一下：

(2)任意子族的元素的并
(3)任意有限子族的元素的交

会更好理解一些。

还有就是，强调“元素的并/交”，意思是说取集合的并和交，在族概念出现后会产生争议。比方说 ，那么如果取（元素的）并就是 ，取并的族就是 ，当然不是一个东西。

在之后还会有诸如“任意的子集的并的族”这样的说法，其实就是对一个集合，取它所有可能的子集，考虑所有可能的并，然后把这些所有可能的并组合为一个族，这个族的元素就是所有的这些可能的并集。

在集合论中，这样复杂的表达是非常多的，因此初见可能有点不习惯。这里给大家打个预防针2333……

好的继续往下看。紧跟着下面的一个定义是这样的

Definition:open set
对于一个集合 ，定义 是一个附有 的一个拓扑空间，如果 ，那么称 是 内的一个开集。

要理解这个抽象的概念有点困难是吗？还好，书上举了大量的例子，我们列举一二。

Example 1
设 ，那么显然， 这就是一个拓扑（定义为平凡拓扑(trivial topology）），显然，取 的所有子集合，构成一个族，它也是一个拓扑。这被定义为离散拓扑(discrete topology)。当然了，对于这个集合， 也是满足条件的一个拓扑。

下图是拓扑的一种图示，可以看出一个椭圆（你画成五角星也行，闭着就可以）其实就代表着一个集合。

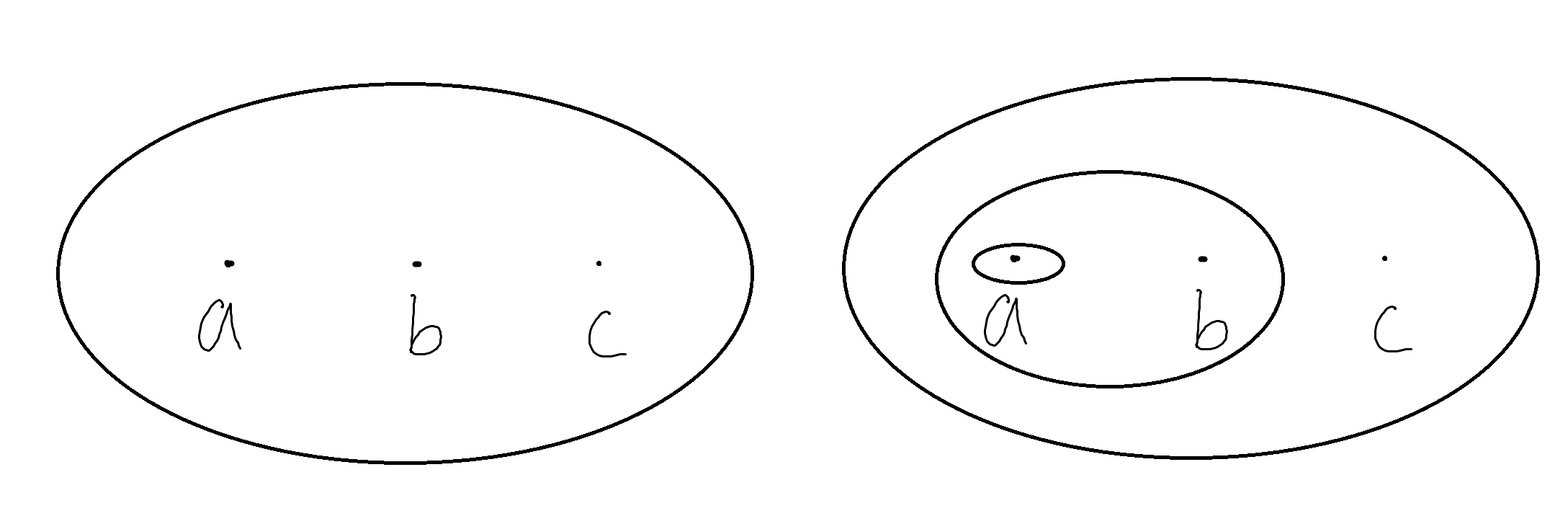
还有一个有趣的例子是这样的

Example 2
设 是一个集合，定义 为所有的满足 ，且 要不是有限集，要不是 本身的 的族，则 是定义在 上的一个拓扑（定义为有限补拓扑）。

我们证明一下这个结论。刚开始学一个抽象的概念，最好的办法莫过于走定义。

首先要证明 是在族内的，因为 ，第一个是 本身，第二个是有限集，所以这个结论是对的。

再设 为任意一个 内的非空元素的族，现在要证明的是 是在这个族内的。这可以通过公式 （De-Morgan）来得到（这个过程我故意跳了，因为我觉得大家可以自己明白为什么这些集合都是有限集）。所以后两个条件也满足，就证明了结论。

下面是拓扑比较常用的几个定义

Definition:finer,coarser(or strictly),comparable
设 是两个定义在 上的拓扑，如果 ，则称拓扑 比另一个更细。如果是真包含，就称它比另一个拓扑严格细。反过来就说拓扑 比另一个粗糙，如果是真子集，就称比另一个拓扑严格粗糙。
如果两个拓扑有包含关系，称这两个拓扑可比较。

这些概念在之后你会发现是很重要的，不过现在我需要先放在这里。

和线性空间一样，拓扑空间也可以用基来去刻画它的结构，我们来看看。

Definition:basis
设 是一个集合，如果一个 的子集合的族 满足
(1)对于每一个 ，存在至少一个元素 满足 。
(2)如果 ，那么存在一个元素 满足 。
则称这个族是一个定义在 上的拓扑的基。

同样的，有了一个基，就可以在 上生成一个对应的拓扑 ，满足：对于任意的 ，对每一个 ，存在一个元素 满足 。

关于拓扑的基，先给两个例子来看看。

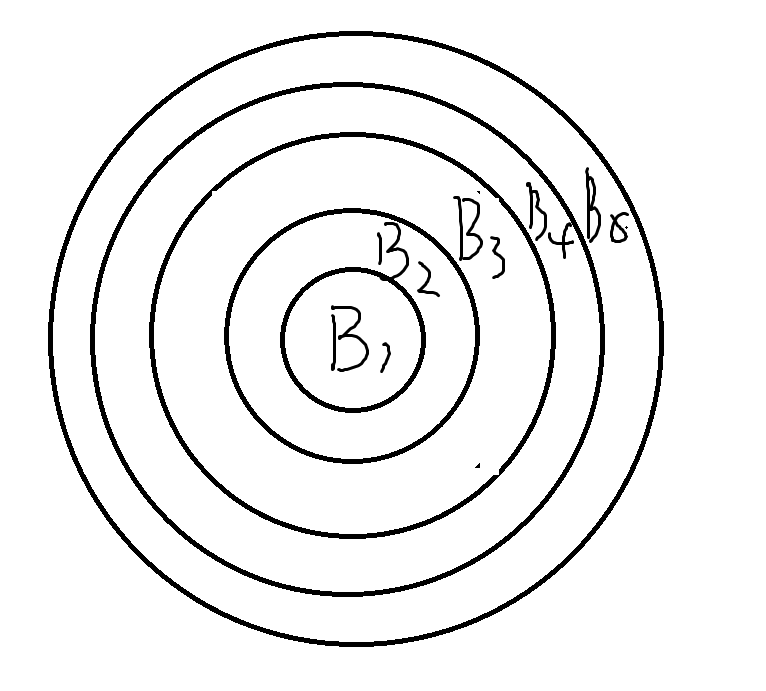
Example 1
考虑设 为整个二维平面，那么定义 为圆心在原点，半径为 的闭圆的内部和边界区域。那么 就是满足条件的一组基。

这个例子的图示如下，注意

书上还给的一个例子其实就是前面我们说的所谓“由基生成的拓扑”，那个到底是不是拓扑呢？

Example 2
对于任意的集合 ，若对每一个 ，存在一个元素 （也称作基元）满足 。则 ，并且这样得到的 是一个拓扑。

我们证明一下这个结论。

根据定义，先要验证 。根据定义，空集是肯定在的（别忘了第一节我们花时间讨论的逻辑），而全集在的原因是，对于任意的 ，都会存在一个基元 满足 ，而根据基的定义 。

之后，取任意一个集合的子族 ，下面证明 是在拓扑内的。这也并不难，因为对于任意的 ，如果 ，那就会存在某一个集合 满足 ，因为 ，所以存在一个基元 满足 ，也就可以推出 ，这样的话，就满足了题目给定的条件，所以 。

稍微麻烦一点的地方在于交，不过我们只需要考虑证明 是在拓扑内的（因为之后的一般情况就可以采用归纳法了），这是因为如果 ，那么 ，因为 ，所以存在两个基元 ，满足 ，且 ，也就是 。而根据基的第二个定义，有 ，所以就有 。也就是说我们找到了这样对应的一个基元。那自然就说明了结论成立。

可以看出，证明一个族是拓扑，严格走定义下来还是非常严密的，所有的条件都用上了……

所以，我们之后定义这个拓扑就是由这个基生成出的拓扑，当然，就有唯一性了。

下面的一些定理可以用来描述基生成的拓扑和相关的性质。

Lemma:
设 是一个集合， 为定义在 上的拓扑 上的基，则 为 的所有的可能的元素的元素的并的族。

首先要注意到的一个结论是：每个基元都是在拓扑内的。所以根据拓扑的定义，它们的并自然还是在拓扑内，也就是说 的所有的可能的元素的元素的并是包含在拓扑内的。下面只要证明反方向即可。

反方向的意思是，对于任意的在拓扑内的元素 ，都可以写成是一种基元的元素的并的形式。而这是很简单的，因为对于任意的 ，根据基的定义，存在一个基元 满足 ，这样的话可以推出 ，就证明了结论。

这就说明了，对于任意的开集 （也就是在拓扑内的元素），它都可以表示为一系列基元的元素的并，但是要注意，一般情况是不唯一的！这是和线性空间中基的定义非常不同的地方。

有了基的概念后，下面要提的这个概念也是比较独特的。

Definition:subbasis
定义一个在 上拓扑的子基 为 的子集的族，并且它们的元素的并是 本身。定义由子基生成的族 为所有可能的有限的元素的交的所有可能的并。

有一件事需要证明的就是：这个族确实是一个拓扑。如何证明？

我们之前说明了，任意一个拓扑中的元素，都可以表示为一系列基元的元素的并。所以只需要说明：这个子基 中所有可能的元素的交的族 是一组基即可。因为我们之前证明了，所有可能的基元的并的族就是它生成的那个拓扑。

要证明它们是一组基，就需要check两个条件。第一个条件是对于每一个 ，一定都存在一个集合 使得 。这是很显然的，因为 中所有集合的元素的并是 ，那么每一个元素 都至少包含于一个集合 中，那根据族 的构造可以知道，它自然包含在一个 中。就证明了结论。

对于第二个条件，我们换一种方式：对于两个基元，它们的交要不是空集，要不还是一个基元。事实上这个是很容易的，因为如果这两个基元都是有限的元素的交，那么给它们俩取一个交集，自然还是有限的元素的交。也就是说，它还是一个基元，就证明了结论。

这个结论相当于在拓扑中考虑到了“有限的交”，而不仅仅是根据基的任意的并的族来构造它生成的拓扑。是另外一种构造拓扑的方式。

Lemma:
设 为一个拓扑空间，对应的拓扑为 。设 是 的开集的族，满足对每一个开集 ，对每一个 ，都存在一个元素 ，满足 ，则 是这个拓扑的基。

看似这个写的就是基的定义，但是看着不代表真的是，我们还是有必要走一遍基的定义的。

对于第一条其实是很简单的，因为 本身就是开集，所以对于每一个元素 ，存在一个元素 满足 ，这就是基的第一个性质，所以结论是成立的。

再看它的第二条定义。假设 ，因为 都是开集，根据拓扑的定义可以得到 是开集。现在只需要走题目条件就可以得到，确实存在一个元素 满足 ，这就证明了第二条。

证明完是基了，证完了吗？显然是没有的，别忘了，我们这只是证出了它是拓扑的基，但是并没有证明出它是“哪一个”拓扑的基。所以还需要check一下唯一性。假设它生成了一个拓扑 ，下面证明两个相同。

一方面，我们假设一个元素 ，那么它是一个开集，那对每一个 ，存在一个元素满足 ，又因为 是拓扑的基，所以这个集合 又是在 里的。

另一方面，再假设一个元素 ，那么这个元素可以被写为一系列基元的并，但是这一系列的基元都是在这个拓扑 内的（因为它们都是开集），所以根据拓扑的定义，它们的并也是在这个拓扑内的。

综合这两个方面，就足够得出两个拓扑相等的结论了。

这个结论事实上可以通过一个拓扑来构造出一组基，之后我们会用到。

很多人会问的问题是：为什么这个地方证明基需要多加一步唯一性的证明？请注意，上一个定理中，如果我们证明出了一组基，并且对这一组基取“基元的任意的元素的并的族”，那根据定义它就是“这一组基生成的拓扑”，已经保证了唯一性。而这里只是证明了是基，但是并没有其余更多的唯一对应拓扑的条件，所以就需要多加一步证明了。

好的，继续往下看。

Lemma:
设拓扑空间为 ，设 分别为拓扑 的基，则下列命题等价：
(1) 比 更细。
(2)对每一个 和每一个包含 的基 ，存在一个基元 ，满足 。

首先来看 。如果要证明拓扑 更细，就需要证明 ，也就是说，对于任意的 ，都可以证出来 。设 ，那么根据基的定义，存在一个元素 ，使得 ，那么根据条件就可以得到，存在一个基元 使得 ，所以就有 ，根据基的定义，可以得到 就证明了结论。

再来看 。现在假设有一个 ，那么根据基本身就是开集，可知 ，所以根据条件， ，因为 是这个拓扑对应的基，所以就存在一个元素 ，使得 ，这就证明了结论。

这个定理相当于告诉我们，如果一个拓扑更细，就说明它的基“更小”，因为更细的那个拓扑，它的基都是原来粗糙拓扑的子集。

下面是一些常见拓扑的例子。不过碍于篇幅，我们会将一部分的拓扑例子放到下一节。

Definition:standard topology,lower limit topology,K-topology
如果 是所有的在实数轴上的开区间的族，则称被这些基生成的拓扑为实数轴上的标准拓扑。
如果 是所有的左闭右开的区间的族，则称被这些基生成的拓扑是实数轴上的下限拓扑。
如果设 是所有的诸如 的数的集合， 为所有实数轴上开区间和诸如 的形式的集合的族，则称被这些基生成的拓扑为实数轴上的K-拓扑。

需要注意到的是，它们的并其实都是实数集。所以这个时候实数集本身就变成了一个拓扑空间。当然了，我觉得你也应该知道它们为什么是一组基，不过下面这个判断法则可能更容易操作：

基元两两之间的交，要不是一个基元，要不就是空集。

我们之前已经使用过一次这样的操作了。

为了分辨出这些拓扑，我们一般会给它们一些记号：第一个标准拓扑记为 ，第二个拓扑记为 ，第三个拓扑记为 。它们三个拓扑其实具有如下的关系。

Lemma
比标准拓扑严格细，但是二者并不是可比较的。

如何证明？考虑它们的拓扑的基。如果要证明更细，就需要说明，对于任意的一个拓扑的基，这个基的基元包含的每一个元素，都会对应另外一个拓扑的基的基元，这个基元也包含这个元素，并且是原来拓扑的基元的子集。从这个定义出发来证明。

首先来看看 ，因为实数具有稠密性，所以对于任意的开区间 ，都会存在一个元素 ，所以就会有一个集合 ，这个集合包含点 ，并且满足 。另一方面，对于一个集合 和一个点 ，我无法找到一个开区间 ，满足 。综合两条即可得到严格细的结论。

再来看看 。首先是给定任意一个集合 ，这个集合本身又是在 内的。另一方面，给定一个特定的集合 ，那么这个集合是包含 的，但是我没有办法找到一个开集满足 。所以这个拓扑也确实比标准拓扑要严格细。

那么，为什么说二者不可比较呢？还是考虑上面的集合。因为集合 是 的，包含 。但是却找不到一个集合 ，满足 。同样的，对于任意的一个集合 ，取一个点 ，那么对于一个集合 ，首先我无法找到一个开集 满足 ，当然我也无法找到一个开集 满足这个要求（想想为什么）。所以两边的基相当于都找到了一个独立的元素，所以其实是相互不包含的。那么自然它们生成的拓扑就不是可比较的了。

这其实就是实数轴上的比较有趣的三个拓扑的例子了。

好的，来看下一个例子——序拓扑

Definition:order topology
设 是一个有简单次序关系的集合，有不止一个元素。设 是具有下列种类的集合的族：
(1)所有 中的开区间 。
(2)所有 中的左闭右开区间 ，其中 是这个集合 的最小元（前提要求 存在）。
(3)所有 中的左开右闭区间 ，其中 是这个集合 的最大元（前提要求 存在）。
满足以上要求的族就是一组基，它生成的拓扑定义为序拓扑。

因为一个集合 可能没有最大元，或者没有最小元。那就可能不存在其中的某一类。所以可能会有一些序拓扑不含其中的某几类，这是允许的。

可以看出，抽象出来的序拓扑的意义下，原来开区间的“开”其实自然对应到了拓扑学中“开集”的概念上。

举几个关于序拓扑的例子。

Example 1
标准拓扑即为在 上定义正常次序关系后的序拓扑。

这是成立的，因为这个标准拓扑包含所有的第一类的集合，并且它没有最大最小元。所以确实是一种序拓扑。

Example 2
集合 上定义字典序，那么它就是一个有最小元的有序集。那么定义 （请不要忘了这个标记什么意思，回去翻笔记），那么 ，那么它上面就可以定义一个序拓扑。

这个序拓扑有意思的地方在它并不是一个离散拓扑，因为有一个 的子集，它并不是开集。这个集合叫 。因为对于每一个包含它的开集，都一定要存在一个基元，它包含 元素，并且这个基元是这个开集的子集。然而每一个包含 的开集，都一定会带上序列 中的元素（想想为什么），又因为每一个基元都是开集，所以基元不可能是 的子集，就矛盾了。

有的人可能疑惑在这个集合对应的开区间是什么，举个例子应该就明白了： 。

与这个例子相对的是下面这个例子。

Example 3
正整数集上定义的序拓扑是离散拓扑。

我们要证明它，其实只需要证明每一个单元素集合是开集即可（因为剩下的集合可以通过并的操作完成，拓扑对并运算是封闭的）。而这是很容易的，因为 ，而这些都是基元，所以自然都是开集。

最后是一个特殊的序拓扑中的概念。

Definition:rays
定义这些集合为单向无界区间：
其中存在闭方向的为单向无界闭区间，不存在闭方向的为单向无界开区间。

为什么说是开区间？因为考虑在不同的集合 中，以 为例。如果 存在一个最大元 ，那么 是一个开集，如果不存在，那么 ，是开集的并，根据拓扑的定义，还是开集。

单向无界开区间很有趣，是因为它们其实构成了这个 上序拓扑的子基。因为每一个单向无界开区间都是这个拓扑中的元素，那么它生成的拓扑自然是原来拓扑的子集。但是反过来，每一个序拓扑的基元，都是单向无界开区间的有限交（想想为什么）。那么单向无界开区间族生成的拓扑又包含了这个原来的拓扑。所以其实就说明了这个结论。

从上面这个结论中也可以看出，要证明是一个子基，一方面证明这个子基的元素本身是开集，另一方面说明原来的基元都可以被表示为子基的有限交即可。

我们的常微老师同时也担任拓扑学的教学工作，他就这么和我们说：研究拓扑学的人往往声音是最大的，因为他们要说很多很多话。确实，拓扑这门课本身非常抽象，又需要很多的说理逻辑的推导，所以其难度也可见一斑。比如我自己在理解拓扑学的时候，就在他书上的表达中纠结了半天……因为他定义本身的表述，就比较的晦涩难懂，所以理解着实费了一些功夫。

不过有趣的地方往往也就是在这些推导上。所以，还是抱着期待的目光，接着往下看吧，哈哈。

感谢大家一直以来的支持，为点赞收藏感谢赞赏的看客比心~~

——————————————————广告——————————————————

本专栏为我的个人专栏，也是我学习笔记的主要生产地。任何笔记都具有著作权，不可随意转载和剽窃。

专栏目录：笔记专栏|目录

想要更多方面的知识分享吗？欢迎关注专栏：一个大学生的日常笔记。我鼓励和我相似的同志们投稿于此，增加专栏的多元性，让更多相似的求知者受益~